Coefficient matrix is not square or is nonsingular. Then normalize this basis to obtain an orthonormal basis.

Solved Use The Gram Schmidt Process To Find An Orthonormal Chegg Com
An orthonormal basis is constructed easily from an orthogonal basis v1vp.
. To obtain an orthonormal basis which is an orthogonal set in which each vector has norm 1 for an inner product space V use the Gram-Schmidt algorithm to construct an orthogonal. Enter sqrt n for n X x2 X3 sqrt 33 sqrt 63 6 B -sqrt 33 sgrt 66 -sgrt 22 sqrt 33 sgrt 66. Take vectors v₁ v₂ v₃ vₙ whose orthonormal basis youd like to find.
Then normalize this basis to obtain an orthonormal basis. Free Gram-Schmidt Calculator - Orthonormalize sets of vectors using the Gram-Schmidt process step by step This website uses cookies to ensure you get the best experience. 2 4 0 4 2 3.
Posted by Seb On November 30 2020 In Linear Algebra Mathematics for Machine Learning. By using this website you agree to our Cookie Policy. Use the Gram-Schmidt Process found here calculate your answer.
Determine whether this is the case in your software. The given vectors form a basis for R3. Coordinates with respect to orthonormal bases.
The Gram Schmidt process is used to transform a set of linearly independent vectors into a set of orthonormal vectors forming an orthonormal basis. Usually its easier to normalize after having applied the Gram-Schmidt algorithm. The standard basis for a space of any dimension is an example of an orthonormal basis.
To obtain an orthonormal basis which is an orthogonal set in which each vector has norm 1 for an inner product space V use the Gram-Schmidt algorithm to construct an orthogonal. Other Math questions and answers. Using the Gram-Schmidt process we get r 11 x 1 4 2 2 2 2 2 1 2 25 5 beginalign color4257b2r_11color4257b2x_1 color4257b2sqrt42222212 color4257b2sqrt25.
Now lets find the orthonormal basis. Orthonormal bases and the Gram-Schmidt process. Begingroup You can apply the Gram-Schmidt process with any inner product.
Kgwhich form an othonormal basis for U. The way we implement Gram-Schmidt for hand calculation we do not normalize our vectors until the last step to avoid all the square roots. Find an orthogonal basis first then normalize the vectors.
A Use the Gram-Schmidt process to find an orthogonal basis from the given basis. Using Gram-Schmidt to find an orthonormal basis for a plane in R3. Use the vectors in the order in which they are given.
Each vector w i is orthonormal to the linear space V i 1. With this we can rewrite the Gram-Schmidt process in a way that would make mathematicians nod and grunt their approval. How do you find an orthogonal basis using Gram-Schmidt.
W1 w2 w3 b Taking as reference the basis vectors found in part a find an orthonormal basis. First find an orthogonal basis then normalize it and you have an orthonormal basis. Such bases are very useful.
Enter sqrt n for n X x2 X3 sqrt 33 sqrt 63 6 B -sqrt 33 sgrt 66 -sgrt 22 sqrt 33 sqrt 6V6. Orthogonal projections can be computed using dot products Fourier series wavelets and so on from these. Apply the Gram-Schmidt Process to obtain an orthogonal basis.
Use the Gram-Schmidt process to find an orthonormal basis for the subspace Use the Gram-Schmidt process to find an orthonormal basis for the subspace of R4 with basis. The GramSchmidt process is a simple algorithm for producing an orthogonal or or-thonormal basis for any nonzero subspace of Rn. Simply normalize ie scale all the vk.
An orthonormal basis is a basis that consists of mutually orthogonal vectors of length 1. If it is compare your softwares output with the solution given in Example. Created by Sal Khan.
Introduction to orthonormal bases. V1 x1 122 v2 x2 hx2v1i hv1v1i v1 102 3 9 122 432343 v3 x3 hx3v1i hv1v1i v1 hx3v2i hv2v2i v2 001 2 9 122 43 4 432343 292919. That simplifies the calculation.
Finding an Orthonormal Basis. U1 u2 u3 c Find the base change matrix from. Use the vectors in the order in which they are given.
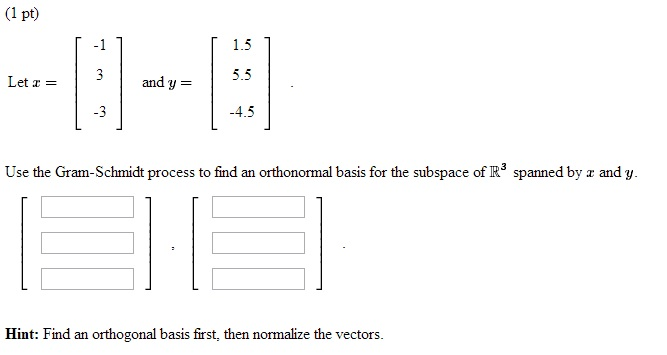
Let x and y Use the Gram-Schmidt process to find an orthonormal basis for the subspace of R3 spanned by x and y. Just replace all u cdot v with. First start with k 2.
Projections onto subspaces with orthonormal bases. Take u₂ v₂ - v₂ u₁ u₁ u₁ u₁ and set e₂ 1 u₂ u₂. Orthonormal basis and the Gram-Schmidt Process We can find an orthonormal basis for any vector space using Gram-Schmidt process.
Take u₁ v₁ and set e₁ 1 u₁ u₁. There is a nice algorithm called the Gram-Schmidt process that will always find an orthonormal basis given a non-orthonormal basis. The Gram-Schmidt process recursively constructs from the already constructed orthonormal set u 1u i 1 which spans a linear space V i 1 the new vector w i v i proj V i 1 v i which is orthogonal to V i 1 and then normalizes w i to get u i w ijw ij.
Given a basis for a subspaceW. It allows us to check whether vectors in a set are linearly independent. The given vectors form a basis for R3.
Using the Gram-Schmidt process we orthogonalize the basis x1 122 x2 102 x3 001. Use the Gram-Schmidt Process found here to calculate your answer. The vectors fu 1u n gform then an orthonormal basis in V.
Let U be a vector subspace of V with U having some basis fu 1u 2g. Apply the Gram-Schmidt Process to obtain an orthogonal basis.

Solved Let X And Y Use The Gram Schmidt Process To Chegg Com

Use The Gram Schmidt Process To Find The Orthonormal Basis For The Row Space Of The Matrix A R Maths

Use The Gram Schmidt Process To Find The Orthonormal Basis For The Row Space Of The Matrix A R Maths
0 Comments